
Cours : définition et calcul du PPCM de deux nombres
Pour comprendre comment calculer le PPCM de deux nombres entiers, Il est important de bien maîtriser la notion de multiple.
Rappel sur le PPCM de deux nombres
Définition du PPCM
Le PPCM de deux nombres entiers est le plus petit commun multiple non nul.
Il est indispensable de préciser 'non nul' car zéro est un multiple de tous les nombres.
Calcul d'une majoration du PPCM
Le multiple commun le plus facilement trouvable à deux nombres `a` et `b` est `a times b`.
Mais ce nombre n'est pas dans la majorité de cas le plus petit multiple commun sauf si `a` et `b` sont premiers entre eux.
Algorithme naïf pour trouver le PPCM
Une méthode pour trouver ce PPCM pourrait être de dresser la liste des multiples de `a` inférieurs ou égals à `a times b` puis de faire la même chose pour `b`, et ensuite de prendre le plus petit multiple commun.
Il existe des méthodes plus efficaces pour calculer le PPCM de deux nombres. Certaines calculatrices possèdent même une touche PPCM comme par exemple la Casio fx-92.
Lien entre le PPCM et le PGCD
Pour `a` et `b` des entiers non nuls, on a l'égalité suivante :
ppcm(`a`, `b`) `times` pgcd(`a`, `b`) ` = a times b`
Exercices : Calcul du PPCM
Cliquer sur le bouton ci-dessous pour visualiser les exercices avec des nombres pris au hasard. Solution détaillée.


Autre algorithme de recherche du PPCM par les multiples
Recherchons le PPCM de 3 et 4.
L'idée sur laquelle repose l'algorithme est de chercher les multiples de 3 et de 4 en favorisant la ligne la plus en retard et de s'arrêter quand les deux lignes sont de la même longueur. comme l'illustre le dessin ci-dessous.
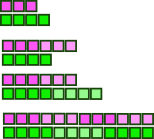
Exemple : recherche du PPCM par les multiples
Un nombre entier `a` non nul possède une infinité de multiples.
`a+a` est un multiple de `a`
`a+a+a` est un multiple de `a`
`a+a+a+a` est un multiple de `a`
`a+a+a+a+a` est un multiple de `a`
...
Existence du PPCM
Soient 2 nombres entiers non nuls `a` et `b`, il existe un multiple commun qui est `a times b`
Démonstration :
`a times b = ` `b+b` ... pendant `a` fois ...` +b`
donc `a times b` est un multiple de `a`
Comme `a times b = b times a ` (voir pourquoi la multiplication est commutative)
L'on en déduit par le même raisonnement que :
`a times b` est un multiple de `b`
ainsi `a times b` est à la fois multiple de `a` et de `b`. L'on en déduit donc qu'il existe un multiple commun puisque `a times b` est un multiple commun évident.
Deux entiers non nuls a et b possèdent une infinité de multiples communs
`a times b` est un multiple de `b`,
`a times b + a times b` est un multiple de `b` car `a times b + a times b = (a + a) times b`
etc...
Exemple de recherche du PPCM avec les listes de multiples
Calculer le `PPCM(12 ; 21)`
L'on sait que le PPCM est inférieur ou égal à `12 times 21` c'est dire à 252.
Voici la liste des multiples de 12 inférieurs ou égals 252 à : 12 ; 24 ; 36 ; 48 ; 60 ; 72 ; 84 ; 96 ; 108 ; 120 ;132 ; 144 ; 156 ; 168 ; 180 ; 192 ; 204 ; 216 ; 228 ; 240 ; 252.
Voici la liste des multiples de 21 inférieurs ou égals à 252 : 21 ; 42 ; 63 ; 84 ; 105 ; 126 ; 147 ; 168 ; 189 ; 210 ; 231 ; 252
Parmis les multiples communs inférieurs ou égals à 252 l'on a : 84 ; 168 ; 252.
Le plus petit multiple communs est dans ce cas 84.
on a donc : `PPCM(12 ; 21) = 84`
Cette méthode qui consiste à trouver la liste des multiples n'est utilisable pas en pratique que sur de petits nombres.
Exercices : additions de fractions
Le résultat est fourni dans la marge de droite.
Cliquer sur le bouton ci-dessous pour visualiser les exercices
Exemple de calcul de PPCM avec la méthode des facteurs premiers
`PPCM(135 ;105)`
Voici les décompositions en facteurs premiers
`135=3^3times5`
`105=3times5times7`
En réunissant les facteurs de `135` et `105`
l'on obtient en gardant les exposants les plus forts :
`3^3times5times7 = 945`
soit `PPCM(135,105) = 945`
L'on peut remarquer que `945` est bien plus petit que le produit de `135` par `105`.
