Comprendre la numération en base 16 (hexadécimal)

Le système hexadécimal est très utilisé dans l'informatique. Par exemple les adresses MAC, les adresse Internet IPv6, les codes couleurs des pages Web, sont exprimés en hexadécimal.

L'une des raisons du succes de l'hexadécimal est qu'il est très facile de passer du binaire à l'hexadécimal et réciproquement.

Savoir compter en base 16, est important pour les informaticiens et aussi pour les enseignants de l'école primaire. Comprendre la base hexadécimale permet de mieux comprendre la base décimale car cela oblige à revoir les mécanismes élémentaires de numération et de calcul que l'on effectue machinalement.

Ensuite nous pourrons passer aux additions posées en hexadécimal qui font souvent partie des exercices du CRPE et des examens des classes d'informatique.

Rappel sur les nombres et les chiffres

Dans la vie courante, nous utilisons tous des nombres que nous écrivons en justaposant dix symboles : les chiffres. Le fait d'utiliser dix chiffres signifie que nous travaillons en base dix.

Les chiffres permettent d'écrire les nombres comme les lettres permettent d'écrire les mots.

Pour écrire un nombre l'on écrit une suite de chiffres dont la position en partant de la droite précise la valeur  (colonnes des unités, dizaine, centaine (i.e. une dizaine au carré), millier (i.e. dizaine au cube)...).

Le nombre vingt-trois s'écrit au quotidien 23 . Le chiffre 3 est placé le plus à droite et a, de ce fait, moins de valeur que le 2 qui est sur la seconde colonne (colonne des dizaines) en partant de la droite.

"23" se décompose en 3 +  2 x10

autre exemple en base 10 :

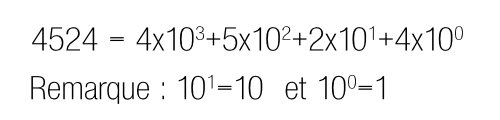
Introduction à la numération en base 16

Dans le cas de la base 16 (hexadécimale), seize chiffres permettent d'écrire les nombres :

0, 1, 2, 3, 4, 5, 6, 7, 8, 9,

A (valeur dix),

B (valeur onze),

C (valeur 12),

D (valeur 13),

E (valeur 14),

et F qui vaut quinze.

Cela permet de compter jusqu'a quinze avec un seul chiffre.

Voyons maintenant comment compter en hexadécimal au-delà de quinze.

Pour compter au dela de quinze, il faut utiliser la notion de 'seizaine' qui désignera une quantité de seize.

Compter en base 16

Voici pour comparer, une liste de nombres à la fois sous les écritures en base 16 et en base 10.

Il faut bien regarder les passages de quize à seize et aussi de trente-et-un à trente-deux.

Seize est le nombre suivant de quinze et il s'écrira avec deux chiffres : Un seizaine et zéro unité : soit en hexadécimal l'écriture suivante : 10.

Le nombre seize s'écrirant donc en base seize : 10.

Si l'on veut chercher à le prononcer il faudra dire 'seize' et non dix ou bien dire 'une seizaine' si l'on veut rapprocher son écriture hexadécimale et sa prononciation.

Le nombre trente-deux s'écrira 20 en base seize que l'on pourrait prononcer : "deux seizaines".

Le nombre trente-quatre s'écrira 22 en base seize.

Ce nombre pourrait se prononcer : "deux seizaines et deux".

Exemple de dénombrement en base 16

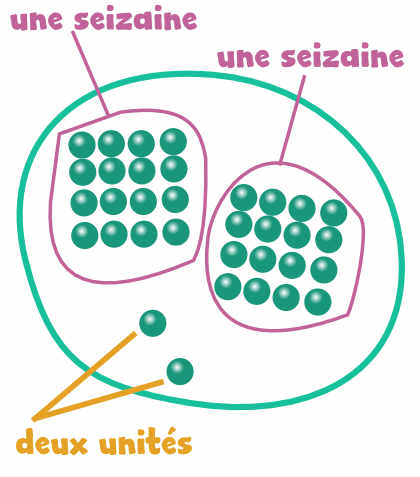
Dans l'exemple ci-contre nous allons chercher à obtenir, écrit en base seize, le nombre d'éléments d'un sac de billes.

En réorganisant les billes en groupements de seize, l'on constate qu'il reste deux billes hors seizaines. Nous utiliserons le chiffre deux pour désigner ces billes là et nous le placerons le plus à droite dans le nombre.

?2

où le symbole ? est à remplacer par un chiffre indiquant le nombre de seizaines.

Si l'on compte le nombre de paquets de seize billes), on en trouve deux.

L'on en arrive à la conclusion qu'il y a

22 (en base 16) billes soit : "deux seizaines et deux" ou plus naturellement trente-quuatre.

Il s'agit du même nombre exprimé dans deux bases différentes. Un nombre existe indépendamment de la base que l'on utilise pour l'écrire.

Question : Que se passe-il lorsqu'il y a plus de seize seizaines ?

Les additions en base 16

Pour aborder les additions en hexadécimal, il faut savoir que la démarche est la même que pour les additions en base dix : il faut connaitre ses tables d'addition en base 16 ou compter sur ses doigts !

Et appliquer les mêmes méthodes que pour la base dix.

Plus d'explications sur les additions en hexadécimal voir : ici

Exercices de calcul en base 16 avec solutions :

additions en hexadécimal,

soustractions en hexadécimal,

multiplications en hexadécimal.