Comprendre la numération en base 5 pour préparer le CRPE

Pour être capable de comprendre le mécanisme des additions posées en base cinq, il faut bien savoir écrire les nombres dans cette base en comprendre le sens. La numération dans differentes bases fait parti du programme du CRPE.

Rappel sur les nombres et les chiffres

Dans la vie courante, nous utilisons tous des nombres que nous écrivons en justaposant dix symboles : les chiffres. Le fait d'utiliser dix chiffres signifie que nous travaillons en base dix.

Pour faire une comparaison avec la langue écrite : les chiffres sont aux nombres ce que les lettres sont aux mots.

Ainsi l'on forme un mot en accollant des lettres. Pour écrire un nombre l'on écrit une suite de chiffres.

ainsi le nombre vingt-trois s'écrit au quotidien 23 . Le 2 et le 3 sont des chiffres pris parmi nos dix chiffres usuels : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Remarque : Il existe des nombres entiers naturels qui ne s'écrivent qu'avec un chiffre : ceux sont les nombres positifs ou nul inférieurs à dix.

Par abus de language, l'on parle souvent de chiffre pair ou impair. Il s'agit en fait d'un nombre à un seul chiffre et cela participe à l'entretien de la confusion entre nombres et chiffres.

Introduction à la numération en base 5

Quand l'on lit un nombre écrit en chiffres, il faut tenir compte de la position des chiffres et de la valeur attribué à un chiffre.

Dans le cas de la base cinq, l'on ne dispose que de 5 chiffres : 0, 1, 2, 3, 4 et c'est tout !

Le dessin à droite illustre le problème qui se pose pour écrire le nombre en base cinq qui correspond au dénombrement d'un ensemble à cinq éléments.

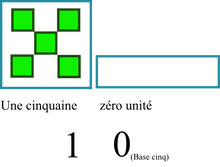
Pour passer le cap d'un ensemble ayant cinq éléments ou plus, il faut inventer la notion de 'cinquaine' qui désignera une quantité de cinq.

Ainsi le nombre cinq pourra se décomposer additivement en 1 cinquaine et 0 hors cinquaine (unités).

Le nombre cinq s'écrira donc en base cinq : 10. Si l'on veut chercher à le prononcer il faudra dire cinq et non dix !

Si l'on veut rapprocher son écriture en base cinq et sa prononciation serait : une "cinquaine" = 10.

Remarque : le mot cinquaine coule de source dans ce contexte mais existe-il ?)

Le nombre dix s'écrira 20 en base cinq que l'on pourrait prononcer : "deux cinquaines".

Exemple simple de dénombrement en base 5

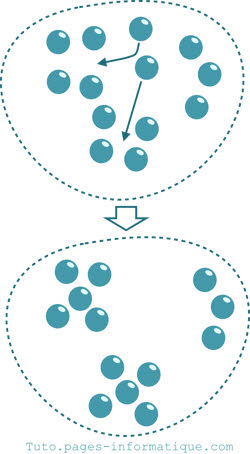
Dans l'exemple ci-contre nous allons rechercher le nombre d'éléments (la cardinalité d'un ensemble) d'un sac de billes et l'écrire directement en base cinq.

En réorganisant les billes en groupements de cinq, l'on constate qu'il reste trois billes hors cinquaines. Nous utiliserons le chiffre trois pour désigner ces billes là et nous le placerons le plus à droite dans le nombre.

?3

ou le symbole ? est à remplacer par un chiffre indiquant le nombre de cinquaines.

Si l'on compte le nombre de cinquaines (le nombre de paquets de cinq billes), on en trouve deux.

L'on en arrive à la conclusion qu'il y a

23 (en base 5) billes soit : deux cinquaines trois ou plus naturellement treize (c'est le même nombre car un nombre existe indépendamment de la base que l'on peut utiliser pour l'écrire).

Problème : Que se passe-il lorsqu'il y a plus de 5 cinquaines ?

Autre exemple dénombrement en base 5

Cette fois, nous avons un sac de carreaux et ils sont plus nombreux.

La première étape consiste à regrouper les éléments par cinq. une fois les regroupements effectués il reste quatre éléments : le chiffre à utiliser pour les unités sera 4.

??4

La seconde étape consiste à prendre les groupements de cinq et à les regrouper par cinq. L'on obtient un super-groupement contenant cinq groupements de cinq et trois groupements de cinq.

Les trois groupements de cinq correspondent à trois cinquaines. Le chiffre à gauche du 4 sera donc 3.

?34

Le nombre de super-groupement contenant cinq groupement de cinq est un. Le chiffre à gauche du 3 sera donc 1.

L'on obtient l'écriture en base 5 suivante :

134

que l'on peut prononcer :

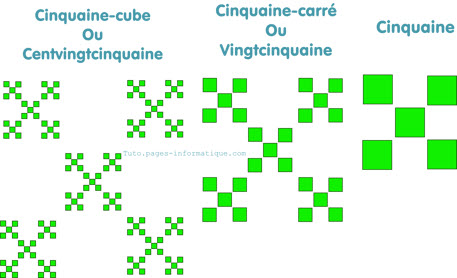
"Une vingtcinquaine trois cinquaine quatre"

ou encore

"Une cinquaine-carré trois cinquaine quatre"

Pour retrouver le nombre en base 10, l'on peut procéder en calculant : (1 x 25) + (3 x 5) + 4

Remarque : Il est interessant de faire la comparaison entre la division euclidienne par cinq et les regroupements par cinq :

Dans un nombre X combien de fois cinq et combien reste-t-il ?

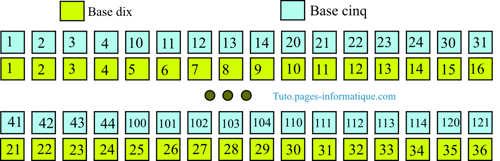
Compter en base 5

Voici pour comparer, uns liste de nombres à la fois sous les écritures en base 5 et en base 10.

Il faut bien regarder les passages de quatre à cinq et aussi de vingt-quatre à vingt-cinq.

Les additions en base 5

Il est temps d'aborder les additions en base 5

Le principe est le même que pour les additions en base dix : il faut connaitre ses tables d'addition en base 5 !

Et appliquer les mêmes méthodes que pour la base dix.

Plus d'explications sur les additions en base 5 cliquez sur le lien ici

Additions posées en base 5 : Exercices avec solutions.