Comprendre pourquoi la multiplication est commutative

Comprendre intuitivement la commutativité de la multiplication

Le fait de pouvoir inverser les termes d'une multiplication nous est tellement famillier que l'on ne se pose plus la question du fondement d'une telle propriété.

Voici sous une forme visuelle et intuitive une correspondance entre trois fois 2 et deux fois  3

Trois fois 2 : 2 + 2 + 2

se tranforme en

3 + 3 : deux fois 3

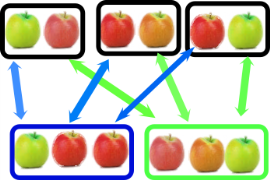
Une autre façon de visualiser la commutativité de la multiplication

 avec l'exemple : 3 x 2 = 2 x 3

est de l'illustrer de la manière suivante

Pour une preuve un peu plus "formelle" de la commutativité

Il faut prouver que : a x n = n x a  pour tout nombre entier n

(h1) supposons que pour tout a et pour tout b strictement inférieurs à n et a et b non nuls on a :

 a x b = b x a

a-t-on  :    a x n = n x a      ?

par hypotèse (h1) on a   0 < a < n

il existe deux nombres strictement positifs c et d tels que n = c + d

on a donc

 c < n  et d < n

ainsi  a x n = a x (c + d)

on a donc  a x (c + d) = a x c  + a x d  (distributivité de la multiplication par rapport à l'addition)

comme on a l'hypothèse (1) et que  c < n  et d < n on a donc a x c = c x a et a x d = d x a

ainsi :  a x c  + a x d = c x a + d x a

et en factorisant : c x a + d x a = ( c + d ) x a  (toujours la distributibité de la multiplication)

donc  a x (c + d) = ( c + d ) x a

comme  c + d = n on a

a x n = n x a

Il est facile de vérifier la propriété pour n = 2 on en conclut que a x n = n x a pour tout n > 1 et a > 1

CQFD.