Comprendre la distributivité de la multiplication par rapport à l'addition

La distributivité de la multiplication par rapport à l'addition correspond à l'égalité suivante :

a x ( b + c ) = a x b + a x c

Pour comprendre cette égalité qui est l'essence de la distributivité de la multiplication, voici une démonstration sur un cas particulier qui utilise des dessins.

Ces illutrations permettent de ressentir intuitivement pourquoi la multiplication est distributive par rapport à l'addition.

Illustration pour comprendre la distributivité de la multiplication par rapport à l'addition

Prenons un exemple vérifions l'égalité : 4 x (3 + 5) = 4 x 3 + 4 x 5

4 x 8 peut se représenter de la manière suivante :

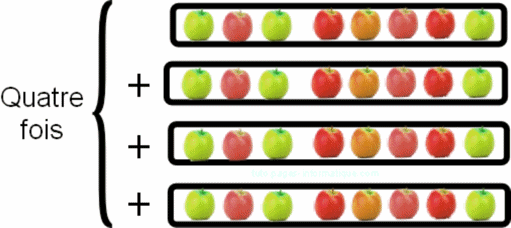
Comme 8 = 3 + 5

chaque rangée de huit pommes peut se découper ainsi : trois pommes + cinq pommes

L'on représente 4 x (3 + 5) comme ci-dessous :

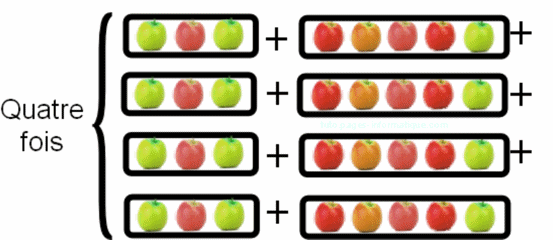
En regroupant chaque colonne comme sur l'illustration ci-dessous, on arrive à l'expression mathématique équivalente :

4 x 3 + 4 x 5

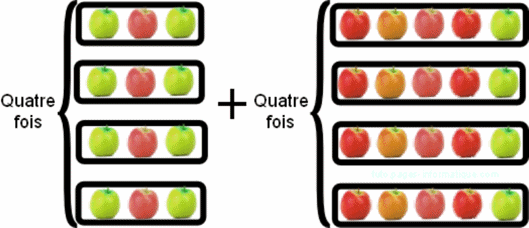
Ainsi l'on peut conclure que 4 x (3 + 5) = 4 x 3 + 4 x 5

Ce raisonnement sur un cas particulier permet de se convaincre de la distributivité de la multiplication par rapport à l'addition.

Voir aussi : comprendre la commutativité de la multiplication

Et aussi la notion de diviseur.