Cours la notion de multiple d'un nombre entier

Exemple de multiples d'un nombre. Lorsque on additionne un nombre à lui même un certain nombre de fois l'on obtient un multiple de ce nombre.

Par exemple pour le nombre 5, les nombres suivants sont multiples de 5.

`5` et que l'on peut écrire `1 times 5`.

`5 + 5` qui est `10` et que l'on peut écrire `2 times 5`.

`5 + 5 + 5` qui est `15` et que l'on peut écrire `3 times 5`

`5 + 5 + 5 + 5` qui est `20` et que l'on peut écrire `4 times 5`

etc...

Définition des multiples d'un nombre

La définition de la notion de multiple est :

Définition

Si A et B sont des entiers naturels.

Si il existe un nombre entier naturel `k` tel que `B = k times A`

Alors Le nombre `B` est un multiple de `A`

et réciproquement

Si le nombre `B` est un multiple de `A`

Alors il existe un nombre entier naturel `k` tel que `B = k times A`

Conséquence de cette définition : le nombre Zéro est multiple de cinq car et on peut écrire `0 times 5`.

Plus généralement `0` est multiple de tous les nombres.

Combien de multiples existe-il pour un nombre ?

Essayons de compter les multiples de 3 de l'ensemble des entiers naturels.

`0 times 3` il s'agit du premier multiple de 3

`1 times 3` il s'agit du second multiple de 3

`2 times 3` il s'agit du troisième multiple de 3

`3 times 3` il s'agit du quatrième multiple de 3

`4 times 3` il s'agit du cinquième multiple de 3

`5 times 3` il s'agit du sixième multiple de 3

`6 times 3` il s'agit du septième multiple de 3

`7 times 3` il s'agit du neuvième multiple de 3

...

En conclusion, on peut dire qu'à chaque nombre entier l'on peut faire correspondre un multiple de 3 et réciproquement.

Il y a autant de multiples de 3 que de nombres entiers.

La relation 'Est multiple de' est transitive

Propriété : La rélation 'Est multiple de' est transitive

Soient A, B et C des nombres entiers naturels.

Si B est un multiple de A

et si C est un multiple de B

Alors C est un multiple de A

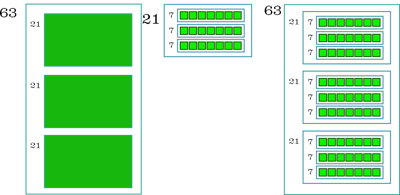
Exemple : 63 est multiple de 21 et 21 est multple de 7

donc 63 est multiple de 7.

Transitivité et multiples d'un nombre entier

Addition des multiples d'un nombre

Propriété : La somme de deux multiples de A est un multiple de A

Soient A, B et C des nombres entiers naturels tels que

B est un multiple de A

et C est un multiple de A

Alors (B + C) est un multiple de A

Par exemple 35 qui est 21 + 14 est un multiple de 7

Attention la réciproque n'est pas vraie :

15 est un multiple de 5 et 15 = 7 + 8

or 7 et 8 ne sont pas des multiples de 5.

Commutativité de la multiplication

Comprendre pourquoi la multiplication est commutative est très utile pour comprendre les multiples et les diviseurs d'un nombre.

Cours : commutativité de la multiplication

Distributivité de la multiplication

Explications : comprendre pourquoi la multiplication des nombres entiers est distributive par rapport à l'addition

Cours : distributivité de la multiplication