Octal : comprendre l'addition en base 8

L'octal est un système de numération autrefois utilisé en informatique qui utilise la base 8. Huit chiffres sont utilisés pour écrire les nombres en octal.

Le mécanisme de l'addition posée en base 8, est le même que pour une addition dans le système décimal aux tables d'additions prés. Ces additions posées en octal peuvent faire l'objet d'un exercice lors du CRPE, ou d'un examen d'informatique. Nous allons expliquer l'addition de deux nombres en base 8 mais avant il est important de bien savoir compter en base 8.

Comparaison entre les additions en base 8 et en base dix

Pour effectuer le calcul 5 + 4 en base dix, il est possible de partir de cinq et d'incrémenter quatre fois.

Voyons cela dans une liste de nombres écrits en base dix. Partons de 5 et additionnons un à un 4 fois de la façon suivante sur la liste ordonnée ci-dessous.

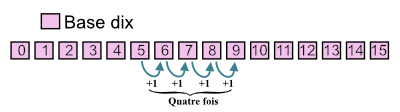
Dans le cas de la base huit, la démarche est identique avec une liste de nombres écrits en octal.

Exemple d'addition posée en octal

Méthode pour additionner les nombres 34 et 45 écrits en octal en posant l'opération.

Remarques :

Le nombre 34 écrit en octal pourrait se lire : trois huitaines et quatre

et le nombre 45 écrit en base huit pourrait se lire quatre huitaines et cinq.

Cette manière de lire les nombres écrit en octal induit une méthode pour les écrire en base dix.

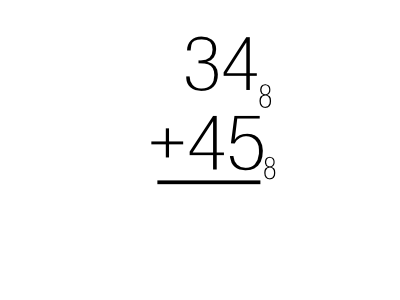
L'on commence par additionner la colonne des unités :

En cherchant dans la table d'addtion de la base huit l'on trouve que 4 + 5 = 11 (une huitaine et un)

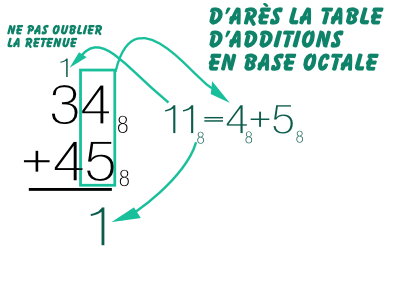
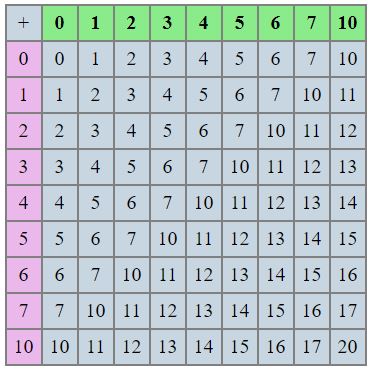
Ensuite l'on addition la colonne des huitaines.

Il faut effectuer le calcul 1 + 3 + 4 dans la base 8. Le 1 provient de la retenue du calcul des unités.

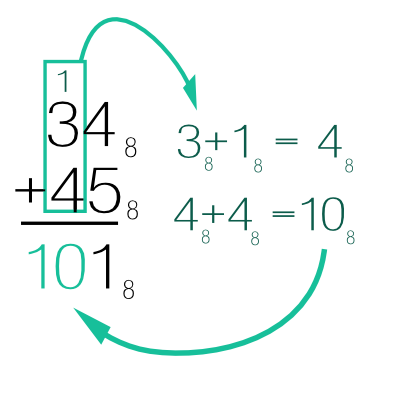
Ce nombre 101 en octal se lirait donc "une huitaine-carré et un". Une huitaine-carré est le nombre 64 (écrit en base 10) auquel on ajoute 1.

Ainsi le nombre 101 écrit en octal est le même nombre que 65 écrit en décimal.

Exercices en base 8 avec solutions